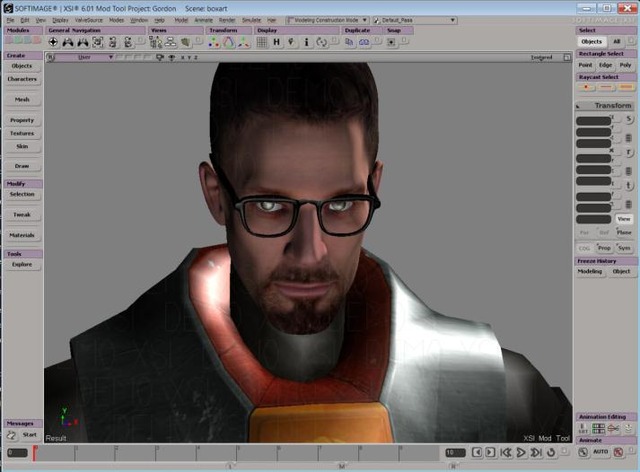
Here's a screenshot of the file used for the final HL2 box art. Seems that all of the Gordon promo material made use of XSI renders for reference material.
 15
15
Here's a screenshot of the file used for the final HL2 box art. Seems that all of the Gordon promo material made use of XSI renders for reference material.
 15
15
That's crazy cool.
wait wtf when did this get leaked? is this the real render??
I thought it was a clean drawing, but it turned out it wasn't. Oh my God)
This feels like seeing a photograph of the real person the mona lisa was painted from
Hey Gordon!
hoping this model gets leaked at some point
softimage moment
I knew they had an official HL2 model of Gordon! I still don't understand why they didn't add him in the actual game
ok but tbh he does look very creepy when i think about it
it looks better then the weird hl1 Gordon with weird texture's
I wish there was a download link
was this model later used for gordon's HL2 survivor model?
Is there anymore like it?
We have an image of the Barnacle artwork's file. It can be assumed the others had files too.
This must have taken a while to render